Mạng nơron – một bộ phận của trí tuệ nhân tạo là một giải pháp mạnh để giải quyết các bài toán phi tuyến phức tạp.

Thăng trầm của trí tuệ nhân tạo là vấn đề của thế giới. Nó không phải là lĩnh vực dễ dàng. Đến với trí tuệ nhân tạo cần hội đủ 3 khả năng: toán học, khoa học máy tính và triết học. Không có toán học thì rất gian nan. Không có khoa học máy tính thì bài toán sẽ trở thành khổng lồ, vì các công thức toán học còn quá đơn sơ so với đòi hỏi của một bài toán mang tính người. Có cả hai nhưng còn thiếu triết lý thì nguy cơ là lầm đường lạc lối, mọi tính toán dễ đi vào bế tắc.

Có hai quan điểm tiếp cận lời giải tối ưu. Lối truyền thống coi vạn vật sinh trưởng như nhau. Chỉ cần cấu hình đủ mạnh, việc còn lại là cải tiến các kỹ thuật để cho ra kết quả. Lối tiếp cận này có ưu điểm là dễ thực hiện vì việc suy dẫn chỉ dựa trên những quy luật đã biết và cấu hình mạnh tự nó thực tế vượt qua nhiều trở ngại. Nhưng quan điểm này có 3 nhược điểm sau đây: cấu hình ấn định trước không thể phù hợp với mọi bài toán đa dạng; cấu hình sử dụng thường cao hơn yêu cầu, như thế sẽ tiêu tốn tài nguyên; không giải được bài toán lớn, đơn giản vì những tiên liệu xuất phát từ đặc điểm phổ thông trong khi lời giải bài toán lại nằm ở nhánh khác của chân lý.

Quan điểm thứ hai coi trọng yếu tố ngẫu nhiên. Rằng một bài toán khó ắt hẳn lời giải của nó phải xuất hiện với xác suất rất thấp. Muốn tăng cơ hội tìm lời giải cần tăng số lượng cấu hình đề xuất, một cách tình cờ. Lối tiếp cận này có rủi ro là nó chứa đựng một không gian lớn hỗn độn các lời giải bao gồm cả những lời giải tồi, do vậy điều quan trọng nhất là phải có biện pháp đánh giá để ngăn chặn những lời giải chất lượng thấp.

Chương trình fpp phiên bản fpp 0.9.6 đi theo lối tiếp cận thứ hai. Chương trình bao gồm 3 tầng xử lý. Xử lý chuẩn(standard processing) dành cho những bài toán thông thường. Tầng này làm việc gần giống quan điểm tiếp cận truyền thống. Bài toán vượt chuẩn sẽ đi xuống tầng thứ hai, đó là tầng xử lý ngoại lệ(exceptional processing). Trong quá trình này fpp đồng thời chọn lọc những lời giải tiềm năng qua xử lý sơ bộ bao gồm thăm dò và thử thách. Những lời giải có kết quả thăm dò thành công và vượt qua được 2000 thế hệ đánh giá sẽ được lưu vào một danh sách động. Đây là một danh sách được tổ chức cấu trúc móc nối để chủ động về cấp phát bộ nhớ và gắn kết muộn(late binding) tùy theo tình hình, dành cho tầng xử lý sau cùng nếu cần thiết, tầng xử lý tiêu điểm(focus processing).

Lấy tầng xử lý ngoại lệ làm ví dụ mô tả. Tầng này quản lý 15 vòng lặp chính, mỗi vòng gồm 30 vòng lặp con, mỗi vòng lặp con có 50 vòng lặp cháu. Tổng cộng có 15x30x50=22500 cấu hình. Một bài toán dễ, thuận logic thông thường, giả sử chỉ cần 1 cấu hình đề xuất với xác suất tìm lời giải thành công là 99%, thì tầng xử lý ngoại lệ dành để giải quyết những bài toán mà với chỉ 1 cấu hình đề xuất, xác suất tìm lời giải thành công là 99/22500≈0.005(%).

Toán học chỉ được sử dụng để điều khiển quá trình học. Còn học cụ thể là do mạng nơron đảm nhận. Đạo hàm hàm lỗi cho biết độ dốc của mặt lỗi tại điểm đang xét. Đạo hàm bậc hai là độ cong của mặt lỗi. Đạo hàm bậc ba là tốc độ biến thiên độ cong và đạo hàm bậc bốn là gia tốc biến thiên độ cong. Các đạo hàm này được dùng để cập nhật trọng số theo hướng hội tụ, giảm sai số và đánh giá chất lượng lời giải cùng với các thông số trọng.

Đạo hàm logarithm

fpp không sử dụng đạo hàm thông thường mà sử dụng đạo hàm logarithm(logarithmic derivation). Chúng ta hãy hình dung một chiếc xe máy tăng tốc trong một giờ từ 60km/h lên 70km/h, và một chiếc máy bay tăng tốc từ 290km/h lên 300km/h cũng trong một giờ. Gia tốc của chúng đều là 10km/h². Vậy sự biến đổi vận tốc của chúng có giống nhau không? Rõ ràng chiếc máy bay có vận tốc cao mà biến đổi bằng với chiếc xe máy là chậm hơn. Cho nên chương trình không khảo sát đạo hàm của hàm số mà khảo sát tỷ số đạo hàm trên giá trị hàm. Đó là đạo hàm logarithm:

y = f(x); [lnf(x)]’ = y’/y

Chúng ta có thể chứng minh điều này dễ dàng sử dụng định lý về đạo hàm của hàm số hợp.

[lnf(x)]’ = (lny)’f’(x) = (1/y)y’ = y’/y

Nếu chỉ như thế thì chúng ta chưa rõ ứng dụng cụ thể của nó. Để thấy được tác dụng của đạo hàm logarithm chúng ta cần thống nhất quan điểm: coi đạo hàm logarithm như một loại đạo hàm riêng, có vai trò như đạo hàm thường, tức là cùng khảo sát biến thiên của một hàm số chứ không chỉ là hệ quả của hàm số hợp. Đối với đạo hàm thường, chúng ta khảo sát số gia của hàm số:

Δy = y2 – y1

Chúng ta hãy xem đối tượng khảo sát của đạo hàm logarithm

Δ(lny) = lny2 – lny1 = ln(y2/y1)

Như vậy, thay vì số gia của hàm số tức là hiệu hai giá trị hàm, đạo hàm logarithm khảo sát tỷ số của chúng.

Đạo hàm logarithm còn cho thấy, một hàm số biến thiên đều và tăng lên, tức là đạo hàm của nó không đổi và dương thì đạo hàm logarithm hay độ tăng trưởng của nó thụt lùi. Để đơn giản chúng ta xét hàm y = x. Đạo hàm logarithm là 1/y = 1/x. Giá trị đối số x càng lớn thì đạo hàm logarithm của nó càng nhỏ dần.

Các ví dụ

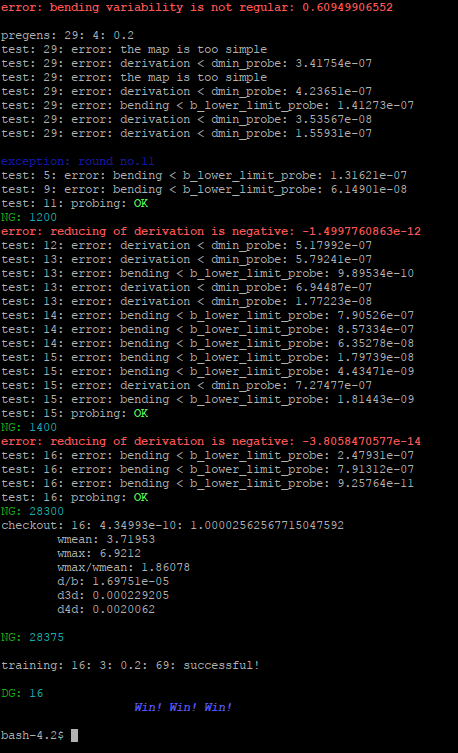
Các ví dụ thể hiện đầy đủ các tầng xử lý. Hình trên cùng ở đầu bài hiển thị kết xuất của bài toán dưới đây. Số liệu soạn ra chỉ để diễn đạt các tình huống, không liên quan gì đến thực tế

-----BEGIN DATA DEFINITION-----
FIRST TEAM: Vietnam Malaysia Japan Macao 
FIRST TEAM HEALTH: Good Medium Bad
FIRST TEAM ACHIEVEMENT: Very-Good Good Medium Bad
WEATHER: Hot Normal Cold Rain
SECOND TEAM: Vietnam Malaysia Japan Macao
SECOND TEAM HEALTH: Good Medium Bad
SECOND TEAM ACHIEVEMENT: Very-Good Good Medium Bad
FIRST TEAM RESULTS: Big-Won Won Lost 
-----END DATA DEFINITION-----

Football predictions data

Orders  FIRST TEAM    Health    Achievement    Weather    SECOND TEAM    Health    Achievement    First team Results
1       Vietnam       Medium    Medium         Normal     Japan          Good      Very-Good      Lost
2       Vietnam       Good      Medium         Hot        Malaysia       Medium    Medium         Won
3       Japan         Good      Good           Cold       Malaysia       Medium    Bad            Big-Won
4       Macao         Medium    Bad            Rain       Japan          Good      Good           Lost
5       Malaysia      Good      Medium         Hot        Macao          Bad       Bad            Won
6       Vietnam       Medium    Good           Hot        Macao          Bad       Bad            Won
7       Vietnam       Good      Medium         Hot        Malaysia       Medium    Medium         Won
8       Japan         Good      Medium         Normal     Vietnam        Medium    Bad            Lost
9       Macao         Medium    Bad            Rain       Japan          Good      Good           Lost
10      Japan         Bad       Bad            Hot        Macao          Bad       Medium         Lost
11      Vietnam       Medium    Medium         Normal     Japan          Good      Very-Good      Lost
12      Vietnam       Good      Medium         Hot        Malaysia       Medium    Medium         Won
13      Japan         Good      Good           Cold       Malaysia       Medium    Bad            Lost
14      Macao         Medium    Bad            Rain       Japan          Good      Good           Lost
15      Malaysia      Good      Medium         Hot        Macao          Bad       Bad            Won 
16      Vietnam       Medium    Good           Normal     Macao          Good      Bad            Lost
17      Vietnam       Good      Medium         Hot        Malaysia       Medium    Medium         Won
18      Japan         Good      Medium         Normal     Vietnam        Medium    Good           Lost
19      Macao         Medium    Bad            Rain       Japan          Good      Good           Lost
20      Japan         Bad       Bad            Hot        Macao          Bad       Medium         Lost

Có hai trận mang kết quả trái ngược là trận số 8 và số 13, đội rất mạnh lại thua các đội yếu. Điều này làm bài toán trở nên khó khăn và chương trình phải trải qua tầng xử lý ngoại lệ ở vòng thứ 11.

Trong trận 8 nếu đổi kết quả Thua(Lost) thành Thắng(Won) thì chương trình sẽ qua hết 15 vòng xử lý ngoại lệ và tìm thấy lời giải ở tầng xử lý tiêu điểm

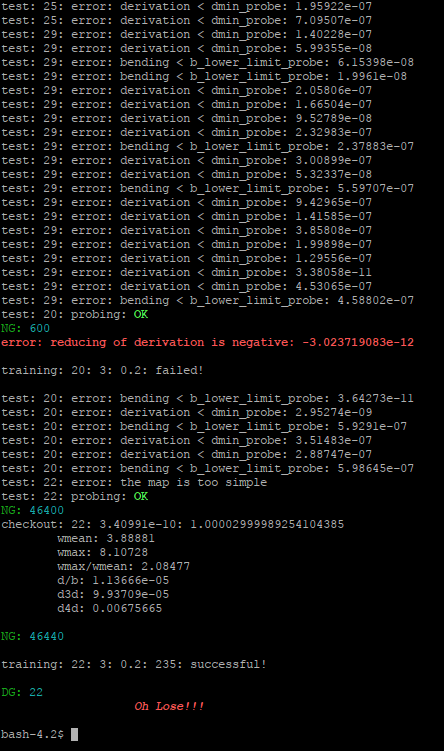
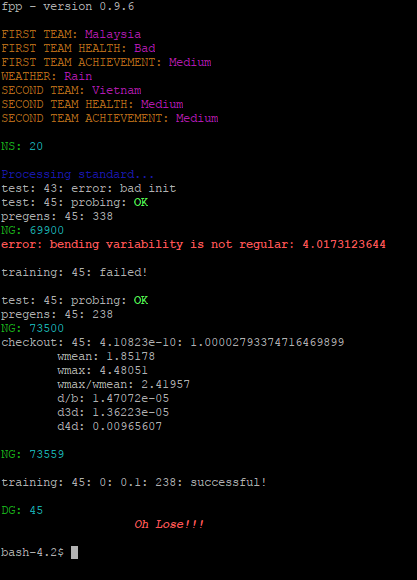
Nếu để nguyên bài toán như lúc đầu rồi đổi kết quả Thua(Lost) thành Thắng(Won) đối với trận 13 thì chương trình sẽ thành công tìm thấy lời giải ở tầng xử lý chuẩn nhưng phải sử dụng cấp học tới mức 45

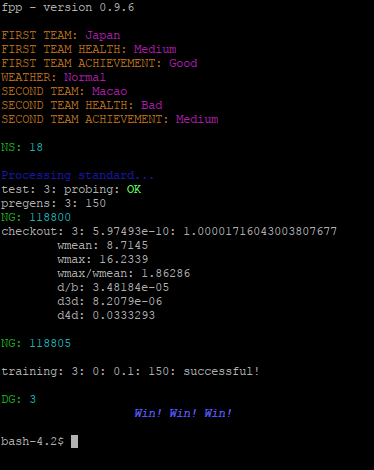
Bây giờ chúng ta bỏ đi cả hai trận 8 và trận 13, các logic ngược không còn, bài toán trở nên dễ dàng và lời giải tìm thấy rất nhanh ngay tầng xử lý chuẩn, chỉ với cấp học mức 3