This article is about the theory of simulating the motion of floating structures at sea, hereinafter referred to as ship.

Simulation is essential, especially when simulating a ship at sea. Simulation eliminates the cost of launching and operating the ship in the marine test field. This is especially true in the case of a suicide USV being required to crash into an enemy’s firepower. At least one physical USV must be sacrificed.
However, the type of simulation required must be a physical simulation(*). All calculations must be accurate based on physical principles with kinematic equations, hydrodynamics, etc. so that the operations are accurately described as they would actually occur.

Archimedes’ Law applies in hydrostatic conditions, when the object is immersed in a liquid in a state of equilibrium. In hydrodynamic conditions, the object is generally not in a state of equilibrium, the center of buoyancy and the center of gravity of the object are not on a vertical line. The Archimedes force does not pass through the center of gravity of the object, in addition to the upward force, it also creates a torque that rotates the object. This torque consumes the force, as a result the upward force is not enough to hold the object as expected.

In addition, there are other forces created by waves and wind acting on the ship. However, the scope of this article only refers to the extended Archimedes force.

We will calculate this force. Suppose:

• F_x is the applied force.

• α is the angular acceleration.

• r is the distance from the center of gravity to the applied point of the force.

• θ is the angle between the direction of the force and the orientation of the distance r.

• I is the moment of inertia of the object about the center of gravity.

We have

F_x = F_translate + F_rotation

The torque formula is T=I×α , on the other hand T=F_rotation×r×sin(θ) so

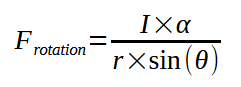
We want the ship to float as if it were in hydrostatic conditions, apply Archimedes’ law

F_translate = F_b = ρ×V×g

Where:

ρ is the density of sea water

V is the volume of water displaced

g is the acceleration due to gravity

Finally, we have the following extended Archimedes’ formula:

Below is a video recording from the simulation program

(*) Physical simulation can be understood as the position and posture of an object are not imposed. Instead, they are the result of forces, torques, frictional forces, moments of inertia, environmental conditions, etc. acting on the object causing changes in motion.