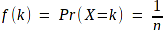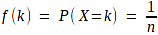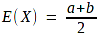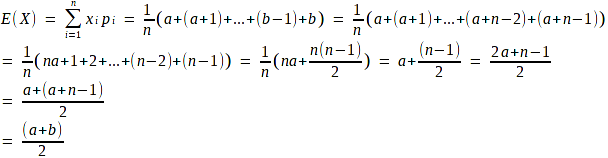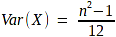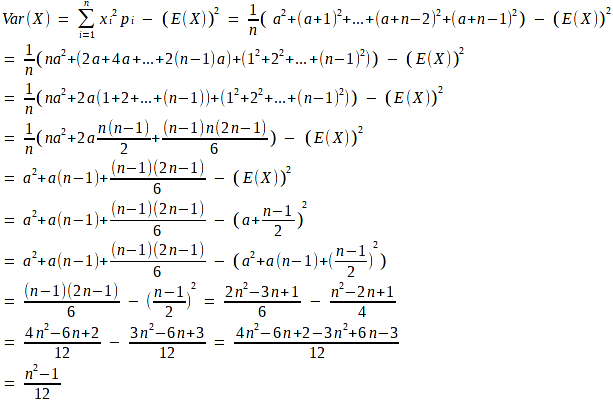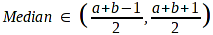Bảng băm trong ví dụ ở bài trước được chia thành 8 ô đánh số ô từ 1 đến 8, biến ngẫu nhiên X là số của ô mà khi băm một khóa vào bảng thì khóa rơi vào ô đó. 80 khóa của bảng được sử dụng như phép thử thực hiện băm khóa 80 lần và chúng ta có mẫu với kích thước là 80.

Definition

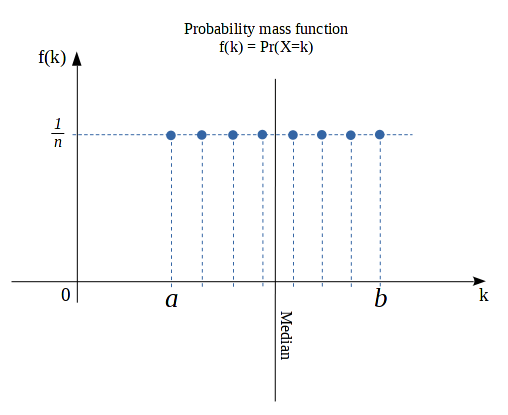
A discrete random variable X is said to have a Discrete uniform distribution through the set A={a, a+1, … , b-1, b}, denoted by U{a, b}, if, for k belong to the set A, the probability mass function of X is given by:

where

• a, b and n are the integers, b ≥ a
• n = b – a + 1, n is the number of elements of the set A

---

Định nghĩa

Biến ngẫu nhiên rời rạc X được gọi là có phân bố đồng đều rời rạc trên tập A={a, a+1, … , b-1, b}, kí hiệu U{a,b}, nếu với k thuộc A, hàm khối lượng xác suất được xác định bởi:

Trong đó

• a, b và n là các số nguyên, b ≥ a
• n = b – a + 1, là số phần tử của tập A

Biến ngẫu nhiên X nhận và chỉ nhận n giá trị rời rạc với xác suất như nhau, bằng 1/n. Nhắc lại ví dụ bảng băm, phân bố khóa đồng đều rời rạc của bảng là phân bố U{1,8}. Số giá trị rời rạc n = 8-1+1 = 8. Trong bài toán kiểm định bảng băm chúng ta chỉ quan tâm bảng phân bố khóa có đều không, chứ không cần giá trị của biến ngẫu nhiên nên các tham số a và b là không có ý nghĩa đầy đủ. Ví dụ nếu đánh số ô của bảng từ 2 đến 9 thì phân bố là U{2,9}, kết quả bài toán không thay đổi, miễn sao n vẫn là 8.

Kỳ vọng (Expected value, Mean)

Vì n = b – a + 1 nên b = a + n -1

Phương sai (Variance)

Trung vị (Median)

Đồ thị hàm khối lượng xác suất trong hình bên trên cho thấy trung vị rất rõ, đường thẳng thẳng đứng đi qua trung vị chia tổng khối lượng xác suất thành hai phần bằng nhau, mỗi phần 0.5.

Nếu n lẻ,

Nếu n chẵn,