Người Việt chúng ta lâu nay vẫn nói ngược về phép chia. 8 : 2 được đọc là 8 chia cho 2, nhưng thực sự phải là 2 chia 8 hay 8 chia bởi 2 (8 divided by 2). Tôi không có ý định sử dụng tiếng Anh để áp đặt vào tiếng Việt vì mỗi ngôn ngữ có cách diễn đạt khác nhau. Vấn đề là ở chỗ câu “8 chia cho 2” sai cả trong ngữ pháp tiếng Việt. Ở đây 8 là đối tượng bị chia và 2 là đối tượng chia, thực hiện chia đối tượng bị chia. Nếu coi ruộng là đối tượng bị chia thì phải là “chúng tôi chia ruộng” chứ không thể nào là “ruộng chia chúng tôi”.

Bạn có thể cho rằng bài viết này chỉ để cho vui vì từ trước tới nay chúng ta vẫn tính được thương số và hiểu thế nào cũng chẳng ảnh hưởng gì. Nhưng nếu như gần 90 triệu người Việt biết phép chia cùng các thế hệ người Việt sau này đều hiểu sai về phép chia thì điều đó chẳng phải là đáng quan tâm?

Trên hết, đó chưa phải là điều quan trọng nhất mà tôi muốn nói tới. Nếu chúng ta không xem xét ý nghĩa của vấn đề mà chỉ cần áp dụng để lấy kết quả thì khó có sáng tạo, và do đó càng khó nâng vị thế của người Việt về khoa học và các thành quả liên quan trên thế giới. Hơn nữa, kết quả như thế mà thiếu đi ngọn nguồn của vấn đề thì có thể chỉ là hình thức và chưa chắc đi vào đời sống.

Tại sao lại như vậy? Bởi vì các ý tưởng sáng tạo dù ban đầu còn rất sơ khai cũng được hình thành từ quá trình tổng hợp các ý nghĩa sâu xa trong cuộc sống, rồi được phát triển trong các giai đoạn sau nhưng luôn bám theo ý nghĩa nguyên thủy để phục vụ trở lại cuộc sống. Cái đó dường như thuộc về triết lý giáo dục.

Quan hệ chia hết

Trong phần bổ sung này, chúng ta phân tích một ví dụ về một vấn đề liên quan, đó là quan hệ chia hết hay quan hệ có thể chia. Quan hệ chia hết được kí hiệu là | (kí tự chia có mã Unicode là 0x2223, tuy nhiên kí tự thanh thẳng đứng có mã Unicode là 0x007C hay được dùng vì gõ tiện hơn). 2 | 8 nghĩa là 2 chia hết 8 (2 divides 8, 8 is divisible by 2).

Chúng ta quan sát poset ({1, 2, 3, 4, 5, 6}, |) với một số đặc điểm sau:

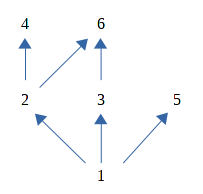
• 1 là phần tử nhỏ nhất vì nó chia hết tất cả các phần tử khác.

• Không có phần tử lớn nhất.

• 4, 5, 6 là các phần tử cực đại.

• 1 cũng là phần tử cực tiểu, và là phần tử cực tiểu duy nhất.

• 4 là một cận trên của {1, 2}, nhưng không phải là cận trên bé nhất của nó.

• 3 là cận trên bé nhất của {1, 3}.

• 2 là cận dưới lớn nhất của {2, 4} và {2, 6}.

• Có ba xích lớn nhất (dài nhất) là {1, 2, 4}, {1, 2, 6} và {1, 3, 6}, chúng đều có chiều dài là 3.

• {1, 5} là một xích cực đại, nhưng không phải là xích dài nhất vì nó chỉ có chiều dài là 2.

• {3, 6} không phải là xích cực đại vì nó là xích con (thực sự) của {1, 3, 6}.

• Chiều cao của poset là 3.

• {2, 3, 5} và {4, 6, 5} là các kháng xích lớn nhất (to nhất), chúng đều có cỡ là 3.

• {2, 3} không phải là kháng xích cực đại vì nó là kháng xích con (thực sự) của {2, 3, 5}.

• {1} là một kháng xích cực đại vì mọi phần tử của {1, 2, 3, 4, 5, 6} \ {1} = {2, 3, 4, 5, 6} đều so sánh được với nó. Hiển nhiên {1} không phải là kháng xích to nhất vì nó chỉ có cỡ là 1.

• Chiều rộng của poset là 3.

• Poset có thể được phân hoạch thành ba xích {1, 2, 4}, {3, 6} và {5}. Số xích phân hoạch như thế bằng chiều rộng của poset. Không thể phân hoạch poset với số xích nhỏ hơn 3.

• Poset có thể được phân hoạch thành ba kháng xích {4, 6}, {2, 3, 5} và {1}. Số kháng xích phân hoạch như thế bằng chiều cao của poset và là số kháng xích nhỏ nhất có thể phân hoạch được. Poset cũng có thể được phân hoạch thành bốn kháng xích {4, 6}, {2, 3}, {5} và {1}. Một phân hoạch thành ba kháng xích khác là {4, 6, 5}, {2, 3} và {1}. Nhưng không thể phân hoạch poset với số kháng xích nhỏ hơn 3, là chiều cao của poset.

PTT